2024. 1. 29. 15:07ㆍ컴퓨터 공학

자료구조
선형 자료구조
배열 : 정해진 크기만큼 데이터가 일렬로 저장되는 정적 자료구조 → 접근,검색,삽입,삭제 가능
연결리스트 : 크기가 정해져 있지 않은 동적 자료구조, 헤드 포인터와 테일 포인터로 시작과 끝을 알 수 있음 → 검색, 삽입, 삭제 가능
스택 : LIFO(후입선출) → 맨 위에 삽입, 가장 위에있는 데이터 삭제 및 확인, 비어있는지 확인, 가득찼는지 확인 모두 O(1)
큐 : FIFO(선입선출) → 맨뒤에 데이터 삽입, 맨앞에 데이터 삭제, 비어있는지 찼는지 확인, 맨 위에 있는 데이터 확인 모두 O(1)
| 시간복잡도/ 데이터구조 | 배열 | 연결리스트 | 스택 | 큐 |
| 접근 | O(1) | X | X | X |
| 검색 | O(n) | O(n) | X | X |
| 삽입 | O(n) | O(1) + O(n)→ 그러나 삽입 위치까지 가는데 O(n)이 걸림 | O(1) → 맨 위에만 | O(1) → 맨 위에만 |
| 삭제 | O(n) | O(1) + O(n) → 얘도 | O(1) → 맨 위에만 | O(1) → 맨 위에만 |
+) 연결리스트는 인덱스로 접근이 가능할까요? No
- 연결 리스트는 추가나 삭제에 시간복잡도가 O(1)이지만 탐색하는데 매번 O(n)이 들어서 일반 배열을 쓰는데에 비해 이점이 없는것같은데 어떤상황에 쓰는거야?
- 동적 크기 조정: 배열은 고정된 크기를 가지지만, 연결 리스트는 런타임에 요소를 추가하거나 제거하면서 크기를 동적으로 조정할 수 있습니다. 이는 메모리를 보다 효율적으로 관리할 수 있게 해줍니다.
- 효율적인 요소 삽입 및 삭제: 연결 리스트에서는 특정 위치에 요소를 삽입하거나 삭제하는 작업이 O(1) 시간복잡도로 매우 빠릅니다. 물론 이를 위해서는 해당 위치에 접근하는 데 추가 시간이 필요합니다. 반면, 배열에서 요소를 삽입하거나 삭제할 때는 다른 요소들을 이동시켜야 하므로 더 많은 시간이 소요됩니다.
- 메모리 할당: 연결 리스트는 각 요소가 메모리의 연속적인 블록에 저장될 필요가 없습니다. 이는 메모리 단편화를 줄이는 데 도움이 됩니다. 배열은 연속적인 메모리 공간이 필요하므로 큰 배열을 생성할 때 메모리 할당이 어려울 수 있습니다.
- 리스트의 크기가 빈번하게 변경될 때: 요소가 자주 추가되거나 삭제되는 경우, 연결 리스트는 배열보다 성능적으로 유리합니다.
- 메모리 제약이 있는 환경: 연결 리스트는 필요한 만큼의 메모리만 할당하므로 메모리가 제한적인 상황에서 효과적입니다.
- 데이터 삽입/삭제 위치가 미리 알려진 경우: 삽입/삭제할 위치가 미리 알려져 있고, 그 위치에 빠르게 접근할 수 있는 경우(예를 들어, 리스트의 시작이나 끝에서 작업할 때) 연결 리스트는 매우 효율적입니다.
- 연결 리스트(linked list)는 특정 상황에서 배열(array)보다 유리한 점이 있습니다. 연결 리스트의 주요 이점은 다음과 같습니다:
비선형 자료구조
1:N , N:N 구조로 데이터가 나열되는 자료구조. 데이터를 하나하나 탐색하지 않아도 찾을 수 있음
그래프
정점(노드) , 간선 → G = (V,E)라고도 표현 사이클 : 한 정점에서 시작해 같은 정점으로 돌아올 수 있는 경로
- 무방향 그래프 : 간선에 방향성 X 그래프, 이때 (A,B)와 (B,A)는 동일한 간선 취급, 정점 n개 일때 간선 최대 개수 n*(n-1) / 2
- 방향 그래프 : 간선에 방향성 O, <A,B>와 <B,A>는 다른 간선 취급, 정점 n개 일때 간선 최대 개수 n*(n-1)
경로 탐색
그래프가 주어졌을때 경로를 탐색하는 방법 두가지
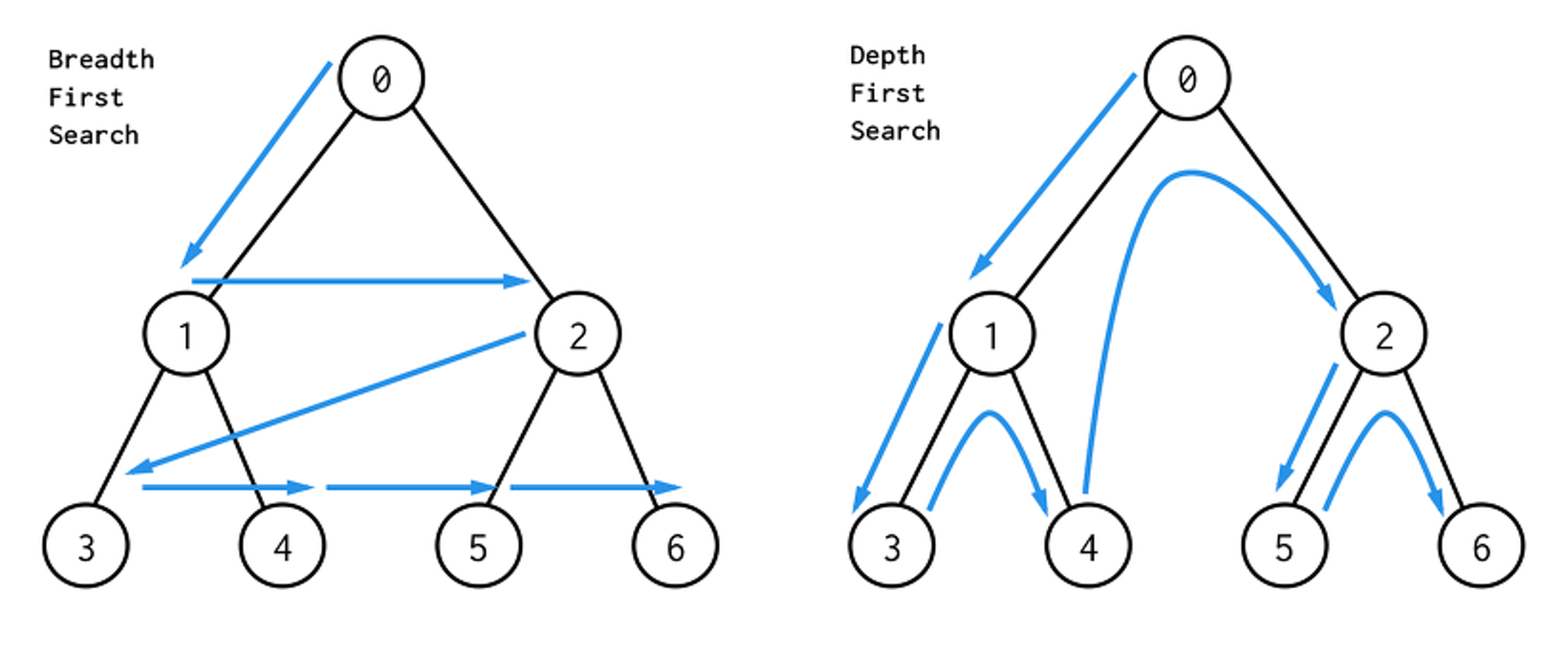
- 너비 우선탐색(BFS) 탐색을 시작하는 정점에서 가까운 정점을 먼저 탐색하는 방식, 먼저 발견한 정점에서 인접한 정점들을 탐색하며 큐에 삽입, 이때 탐색한 정점에 재방문하지 않도록 탐색한 정점을 따로 체크해둬야한다 → 이러한 방식으로 정점에서 정점까지 최단 거리를 알 수 있음
- 깊이 우선탐색(DFS) 시작 정점에서 탐색 가능한 최대 깊이의 정점까지 탐색함 최대 깊이인 정점에 도달했다면 방문한 정점들을 역순으로 재방문, 재귀 호출 또는 스택으로 구현, 최대 깊이까지 탐색 완료시 스택에 있는 정점 하나씩 꺼내며 추가로 방문가능 정점 확인 → 백트래킹????
트리
그래프의 한 종류, 사이클이 없어서 계층적 관계를 표현 가능

이진 트리 : 자식 노드가 최대 2개인 트리
- 완전 이진 트리 : 트리의 마지막 레벨을 제외하고 모든 레벨 노드가 채워져 있음, 왼 → 오 순으로 채움
- 포화 이진 트리 : 마지막 레벨까지 노드가 모두 채워져 있는 이진 트리(= 완전 이진 트리와 같음)
- 이진 탐색 트리 : 같은 레벨일때 왼쪽 노드는 오른쪽 노드에 비해 값이 작아야함 → 특정 값을 검색할때 O(logN) 소요
우선순위 큐
힙 → 이진 탐색 트리 → 상하의 규칙이 있는 이진탐색트리
해시테이블
→ 검색을 자주 사용하는 풀이 과정에서 해시테이블 사용
해시셋
[’a’, ‘b’, ‘c’] , [1,2,3] → arr
{a:1,b:2,c:3} → 검색 자주해야하는 로직에선 무조건 해시테이블
정렬 알고리즘
비교하는 정렬 알고리즘
- 버블 정렬 : 한개의 값을 기준으로 잡고 뒤의 값과 비교하며 크기 순으로 정렬 → 시간복잡도 O(n^2), 단 별도의 메모리 공간이 필요하지X
- 선택 정렬 : 배열을 순회하며 최소값을 찾고 최소값을 맨앞으로 이동시킴 → O(n^2), 메모리공간 X
- 삽입 정렬 : 특정 인덱스가 제값에 가기위해 이전 정렬된 부분에 자기 위치가 될만한곳에 위치시키는 구조 → O(n^2)
- 합병 정렬(머지소트) : 배열을 쪼개고, 분할한 배열을 정렬하며 하나로 합병(최소단위인 2에서부터 비교 후 합치고, 4에서 비교후 합치고 하는 방식) → O(n log n) = 배열정렬시간 O(n) + 합치는시간 O(log n)
+) 합병 정렬과 퀵 정렬은 둘다 분할 정복 알고리즘이다
- 퀵 정렬 : 하나의 피봇을 정해 해당 피봇보다 작은값으로 구성된 배열과 큰값으로 구성된 배열로 분할해 정렬하는 방식 → O(n log n), 최악의 경우 O(n^2)
https://ko.wikipedia.org/wiki/퀵_정렬#/media/파일:Sorting_quicksort_anim.gif
- 힙 정렬 : 최대 힙, 최소 힙 등 자료구조를 이용한 정렬 → O(n log n)

https://yozm.wishket.com/magazine/detail/2312/
비교하지 않는 정렬
- 기수 정렬 : 낮은 자릿수부터 정렬 수행(일의 자리수 기준으로 정렬 후 십의자리 수를 기준으로 정렬) , 버킷이라는 큐를 생성하므로 추가 메모리가 필요 → 데이터개수 n, 최대 자릿수 d일때 O(dn) 걸림
- 계수 정렬 : 데이터 개수를 세서 정렬하는 방식 → O(n+k) → 이해못함 뭐라는겨
최소 신장 트리(MST)
그래프가 이리저리 연결되어있을때 어떻게 연결되어야 가중치가 제일 작고, 모든 정점을 포함하게 할 수 있는지 = 이게 스패닝 트리
즉, 가중치가 있는 그래프에서 간선의 가중치 총합이 가장 작은 신장 트리
프림 알고리즘 : 그리디 알고리즘, 임의의 정점을 시작점으로 트리를 확장하며 MST를 생성 → 힙을 사용
+) 그리디란? 각 단계에서 최선의 선택이 모여 전체의 합이 최선이 되는 알고리즘
- 앞에서 선택한 결과가 나중의 선택에 영향을 주지 않고
- 지역적인 문제에 대한 최선의 선택이 전체적인 문제에 대해서도 최적의 선택이되는 문제여야함
→ 그런데 이런 방식이 MST에서 진짜 최적의 해를 보장하나?
- 사이클 방지: 프림 알고리즘은 이미 선택된 정점들로만 구성된 집합을 확장해 나가기 때문에, 선택된 간선들이 사이클을 형성할 수 없습니다. 즉, 항상 신장 트리의 속성을 유지합니다.
- 최소 가중치 간선 선택: 각 단계에서 가능한 간선들 중 최소 가중치를 가진 간선을 선택함으로써, 최종적으로 구성된 신장 트리의 총 가중치가 최소가 됩니다.
- 컷 속성(Cut Property): 프림 알고리즘은 컷 속성을 만족합니다. 컷 속성이란 그래프의 두 부분을 나누는 컷(cut)에 대해, 한 부분에 있는 정점과 다른 부분에 있는 정점을 연결하는 간선들 중 최소 가중치를 가진 간선을 선택하면, 그 간선은 최소 신장 트리에 포함되어야 하는 간선임을 의미합니다.
크루스칼 알고리즘 : 얘도 그리디 알고리즘, 간선을 오름차순으로 정렬한 뒤 가중치가 낮은 간선부터 선택하며 최소 신장 트리를 생성, 특정 간선을 선택했을때 사이클이 생성된다면 연결하지않고 다음으로 가중치가 낮은 간선을 확인함 → 프림 알고리즘과 달리 간선을 기준으로 트리 생성
→ 유니온 파인드 알고리즘 : 2개의 원소가 같은 집합에 속하는지 판단하는 알고리즘, 크루스칼 알고리즘에서는 두 정점을 선택하고 두개가 다른 그래프에 속한다고 판별되면 두 정점을 연결하고 같은 그래프면 연결 안하도록 하는 알고리즘
최단 거리 알고리즘
정점 간 최단 거리를 구하기 위한 알고리즘
특정 정점에서 다른 정점들까지의 최단 거리
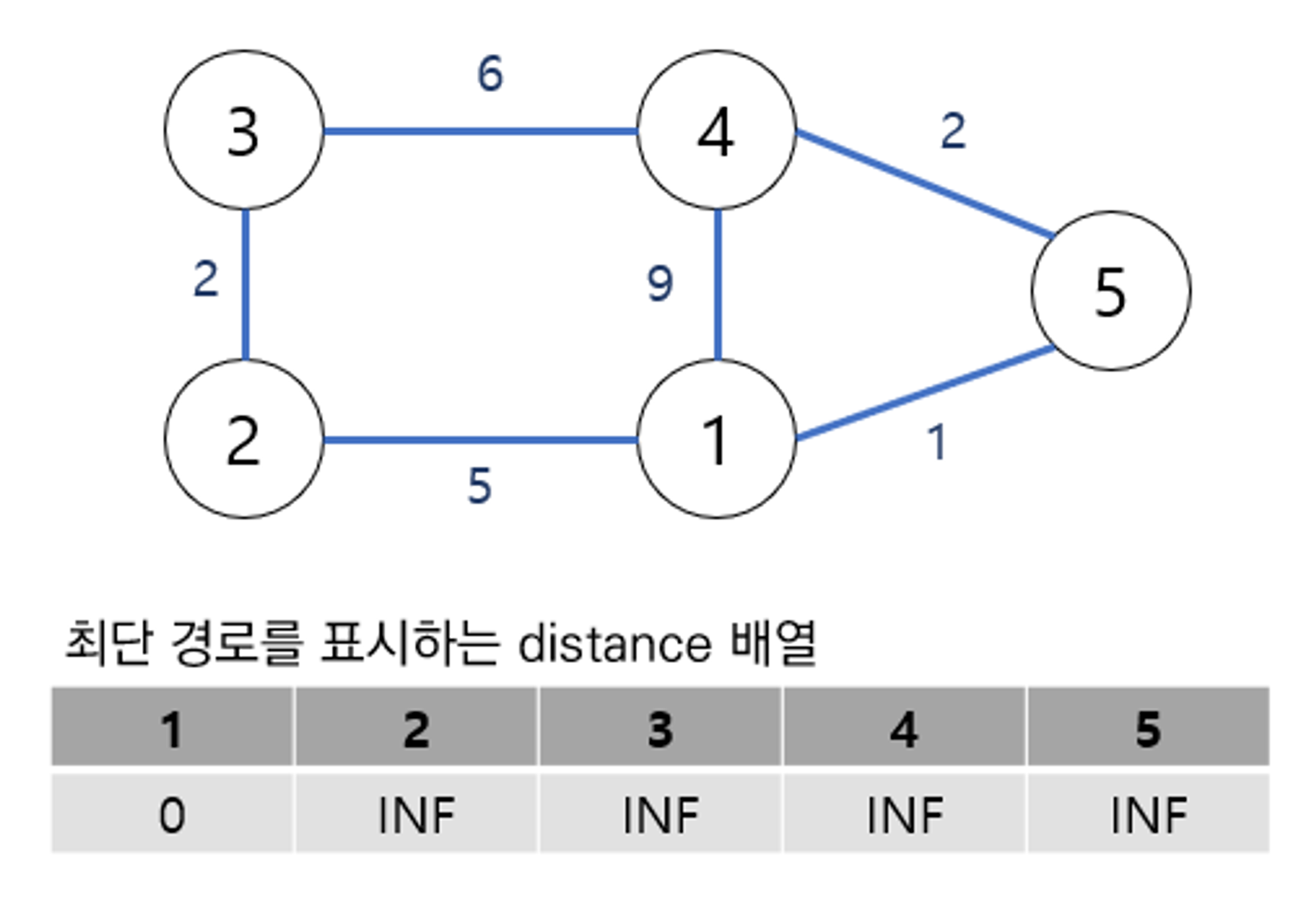
다익스트라 알고리즘 : 간선의 가중치가 음수가 아닌 경우 특정 정점에서 다른 정점까지의 최단 거리를 구하는 알고리즘, 시작 정점을 설정하고 방문 가능하면서 비용이 가장 적게 드는 정점에 방문해 비용을 갱신 → 이때 우선순위 큐를 사용하면됨 (우선순위는 거리를 기준으로!)
그러니까 DP스럽게 푼다고 보면됨. 하나의 정점에서 출발해서 다음 정점으로 갔을때 그 다음 정점에서 나머지 노드들을 방문하는 가중치의 합이 이전노드가 직접 방문한 값보다 작다면 가중치의 합 array에 갱신해주면 되는것
벨만 포드 알고리즘 : 가중치가 음수여도 적용할 수 있음, 음의 사이클이 있으면 최소 비용이 무한하게 줄어들어서 알고리즘 적용X
이해못해서.. 나중에 볼것 추가 +) https://www.youtube.com/watch?app=desktop&v=Ppimbaxm8d8